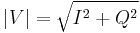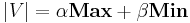Alpha max plus beta min algorithm
The alpha max plus beta min algorithm is a high-speed approximation of the square root of the sum of two squares. That is to say, it gives the approximate absolute magnitude of a vector given the real and imaginary parts.
The algorithm avoids the necessity of performing the square and square-root operations and instead uses simple operations such as comparison, multiplication and addition. Some choices of the α and β parameters of the algorithm allow the multiplication operation to be reduced to a simple shift of binary digits that is particularly well suited to implementation in high-speed digital circuitry.
The approximation is expressed as:
Where 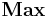 is the maximum absolute value of I and Q and
is the maximum absolute value of I and Q and 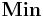 is the minimum absolute value of I and Q.
is the minimum absolute value of I and Q.
For the closest approximation, the optimum values for 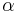 and
and 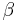 are
are 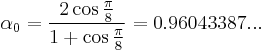 and
and 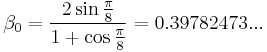 , giving a maximum error of 3.96%.
, giving a maximum error of 3.96%.
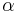 |
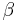 |
Largest error (%) | Mean error (%) |
|---|---|---|---|
| 1/1 | 1/2 | 11.80 | 8.68 |
| 1/1 | 1/4 | 11.61 | 0.65 |
| 1/1 | 3/8 | 6.80 | 4.01 |
| 7/8 | 7/16 | 12.5 | 4.91 |
| 15/16 | 15/32 | 6.25 | 1.88 |
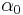 |
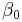 |
3.96 | 1.30 |
References
- Lyons, Richard G. Understanding Digital Signal Processing, section 13.2. Prentice Hall, 2004 ISBN 0-13-108989-7.
- Griffin, Grant. DSP Trick: Magnitude Estimator.